遊泳バクテリアの群れ運動がカオス的流動に至る道筋を解明

2025年3月18日公開

集団運動の制御でアクティブ流体デバイスなどの設計に貢献

プレスリリース研究物理学数理・計算科学生命理工学

ポイント

遊泳バクテリアの群れの集団運動が乱流状態へと遷移する過程で、渦の回転方向の反転・振動状態が最初に現れることを発見。
異なる半径の円形領域内のバクテリア集団を同時観察し、渦が不安定化する転移点近傍でのダイナミクスを詳細に解明。
アクティブマターの集団運動の普遍的な制御理論として、アクティブ流体デバイスやバイオセンサーなどの設計指針に貢献。

概要

東京科学大学（Science Tokyo）^※理学院物理学系の西口大貴准教授（研究当時：東京大学大学院理学系研究科物理学専攻助教、現：同客員研究員）、東京大学大学院理学系研究科の白谷空大学院生、竹内一将准教授、米国ペンシルバニア州立大学のイゴール・S・アランソン（Igor S. Aranson）教授（研究当時：東京大学大学院理学系研究科GSGC教授兼任）らの研究チームは、高密度の遊泳バクテリア^[用語1]懸濁液で見られる集団運動状態が、乱れた時空カオス^[用語2]的な流動を示すアクティブ乱流^[用語3]状態へと至る道筋を解明しました。

高密度の遊泳バクテリア懸濁液では、渦が多く存在し、時空カオス的な流動を示す集団運動状態であるアクティブ乱流が生じます。このバクテリア懸濁液を小さな円形領域内に閉じ込めると、一方向に安定して回転する定常な渦を形成します。本研究では、この円形領域の半径が大きくなるにつれてアクティブ乱流へ至る過程において、まず定常な渦が乱れるとともに渦の回転方向が周期的に反転することを発見しました。また、そうした観測結果を数値計算と解析的理論からも検証し、整合性のある結果を得ました。

本研究では、群れのカオス的な運動に幾何学的な制約を課すことで安定な渦構造へと変換し、さらにその渦構造を周期的に反転する状態へと変換する方法を解明しました。こうした理論は、バクテリア集団だけでなく、培養細胞や他の自己駆動コロイド^[用語4]などの集団にも普遍的に適用できるため、新たなアクティブ流体デバイスなどの設計指針となると期待されます。

本成果は、3月14日付（現地時間）の「Proceedings of National Academy of Science（米国科学アカデミー紀要）」に掲載されました。

2024年10月1日に東京医科歯科大学と東京工業大学が統合し、東京科学大学（Science Tokyo）となりました。

図1. 乱雑な集団運動を示す遊泳バクテリア（左）の高密度懸濁液を異なる半径の円形領域内に閉じ込めた（右）。それらの挙動を比較した結果、半径が大きくなるに従って、定常な単一の渦が徐々に不安定化して時空カオスに至る道筋を解明した。

背景

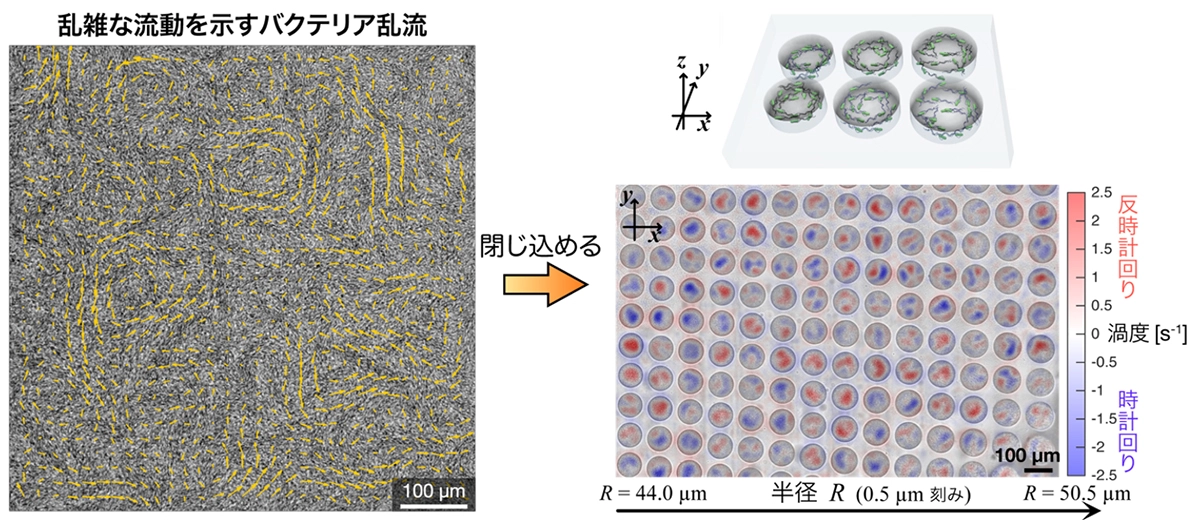
鳥や魚の群れや、微生物のコロニー、培養細胞集団などのように、自ら動き回る要素が集まってできた集団を1つの物体とみなしてアクティブマターと呼び、これらに共通する普遍法則を見出そうとするアクティブマター物理学が、この30年ほどで発展してきています。アクティブマターでは、自ら動き回る要素同士が相互作用した結果、互いに向きを揃えて群れをなして運動する集団運動が多様な実験系で観察されています。そうした集団運動の中でも、遊泳バクテリア集団や分子モーター集団、自己駆動コロイド集団などで広く観察されるのが、速度場（流体や粒子集団などの速度を、空間の各点xと時刻tの関数として表したもの）に時空カオスが生じて渦が多く存在する、アクティブ乱流という集団運動状態です。特に遊泳バクテリア集団で見られるアクティブ乱流をバクテリア乱流と呼び、アクティブマターの集団運動の典型例として、その統計的性質などが詳細に調べられてきました。

アクティブ乱流の性質として、渦が乱雑に行き交っているものの、その渦には特徴的なサイズが存在します。その結果、アクティブ乱流を示す遊泳バクテリア集団などを、その特徴的な渦サイズに合致する円形領域に閉じ込めると渦が安定化し、1つの渦が円形領域内で安定に存在し続けることが知られています。このようなアクティブ乱流の閉じ込めという幾学何的な制約を課すことで、乱れた流れを整流し、整った運動を引き出せます。一方で、この閉じ込めを弱くしていく、つまり円形領域の半径を大きくしていくと、やがて十分大きな半径において、閉じ込めていないときに観察されるアクティブ乱流が生じると予想されます。このアクティブ乱流に至る遷移過程において、どのように渦が乱れていき、どのような中間状態が現れるのかという乱流化シナリオに関する基礎的な理解はこれまで得られていませんでした。

このような整った流れから乱れた流れに至る道筋についての理解は、水や空気などの通常の流体での乱流研究においても根幹をなす重要課題です。乱流への遷移過程の解明は、乱れを抑制する、あるいは利用するうえで必要不可欠な理論的基盤を与えます。

研究成果

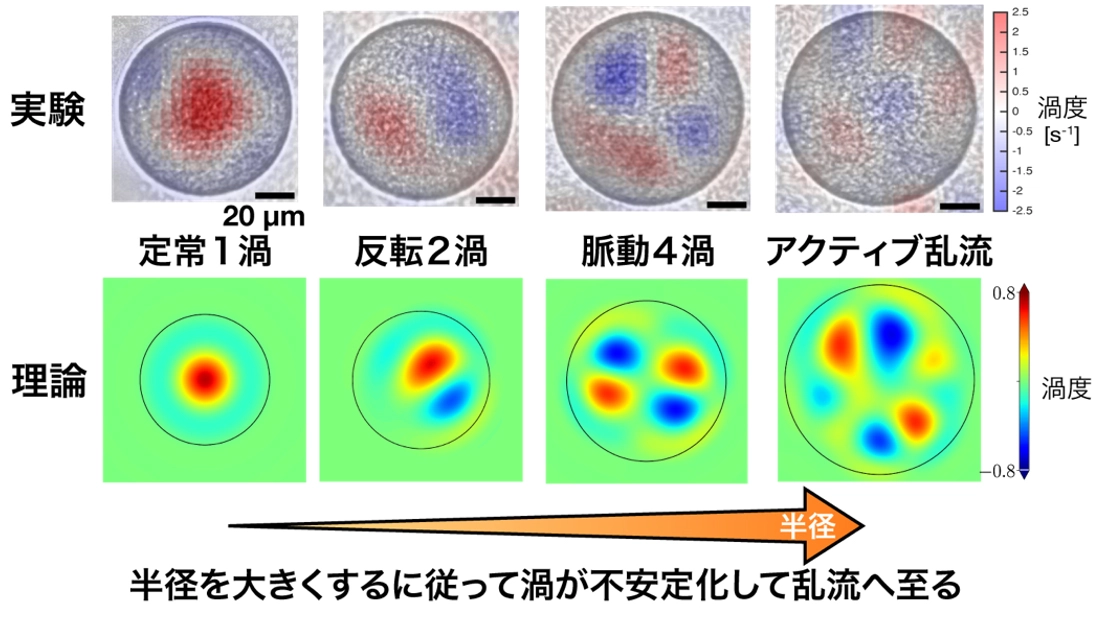
本研究ではまず、微細加工技術^[用語5]を用いて異なる半径の円形領域を多数作製し、それぞれにバクテリア乱流を示す遊泳バクテリアの高密度懸濁液を閉じ込めて、同時観察しました（図1、動画1）。そうした半径が異なる円形領域内のバクテリア集団の挙動を比較した結果、半径が大きくなるに従って、定常な単一の渦が徐々に不安定化していくことを突き止めました。具体的には、まず円形領域内で2つの渦が競合した結果として、領域内全体の回転方向が周期的に反転するという不安定性が生じます（図2、動画2）。さらに半径を大きくしていくと、円形領域内に4つの渦が共存し、その配置が脈動的に変動する挙動を示すようになります。これらの遷移過程を経て、最終的には大きな半径において時空間的に乱れた乱流状態へと至ることが判明しました。

次に、これらの実験での観測結果を、バクテリア集団運動の速度場を記述する連続体方程式を用いた数値計算により再現することにも成功しました。さらに解析的な計算により、この遷移過程の数学的な性質と不安定化のメカニズムを力学系理論^[用語6]の観点から明らかにしました。これにより、実験・数値計算・解析的理論のいずれにおいても、渦の反転周期の半径依存性などにおいて整合する結果が得られたことになり、渦の安定化および不安定化の条件を理論的に予言できるようになりました。

図2. 半径が異なる円形領域に閉じ込められたバクテリア集団の渦の挙動の比較。渦の回転方向の反転と振動が現れたのちに、時空間的に乱れた乱流状態へと至ることをとらえた。

社会的インパクト

本研究で明らかになった渦の不安定化原理とアクティブ乱流へ至る道筋は、普遍的な理論と考えられ、バクテリア集団に限らず、アクティブマター実験系に広く適用可能であると期待されます。また円形領域だけでなく、他の幾何形状でも同様の理論的な記述によって不安定性を理解できると考えられます。本研究で解明した、アクティブなエージェントの集団運動に対して、幾何学的な制約で運動を制御して整流する方法や、不安定性を引き起こす機構は、微小スケールでの撹拌や物質輸送を実現する、群れをなす自己駆動粒子^[用語7]の集団を用いたアクティブな流体デバイスやバイオセンサーなどの設計への活用が期待されます。

今後の展開

研究チームは、今回解明したアクティブ乱流への道筋のさらなる数学的な特徴付けやノイズの効果の定量評価、さらに遷移過程で現れる渦が周期的に反転する状態を活用する研究を進めています。これにより、微生物の集団運動をより高度に制御し利用する方法論の提案を目指しています。

付記

本研究は、科学技術振興機構戦略的創造研究推進事業さきがけ（西口大貴：JPMJPR21O8）、科学技術振興機構創発的研究支援事業（竹内一将：JPMJFR2364）、日本学術振興会科学研究費助成事業（西口大貴：JP19H05800、JP20K14426、JP23K25838、白谷空：JP24KJ0890、竹内一将：JP19H05800、JP24K00593）、日本学術振興会先端拠点事業 “Advanced core-to-core network for the physics of self-organizing active matter (JPJSCCA20230002)”、アメリカ国立科学財団（Igor S. Aranson：PHY-2140010）による支援を受けています。

用語説明

[用語1]: 遊泳バクテリア：大腸菌や枯草菌などの典型的な実験用バクテリアは、らせん型のべん毛が体から生えており、それらを回転させてスクリューの原理で泳ぎ回る。
[用語2]: 時空カオス：時間的にも空間的にも不規則で乱雑な変動を示す現象のこと。
[用語3: アクティブ乱流：バクテリア集団や培養細胞集団などのように、ミクロなスケールのアクティブマターにおいて見られる時空カオス的な集団運動のこと。
[用語4]: 自己駆動コロイド：電気エネルギーや化学エネルギーを消費して自ら泳ぎ回る微小な人工粒子のことで、典型的には数マイクロメートル（µm）程度の直径を持つ。バクテリアなどの生物実験系と並び、アクティブマター研究の重要な対象である。
[用語5]: 微細加工技術：微小な構造を作る技術の総称。本研究では、紫外線で硬化する樹脂（フォトレジスト）をパターン照明で露光することで数十 µmから数百 µm程度の構造をシリコンウェハー上に作製し、その構造をシリコーン樹脂に転写し造形するソフトフォトリソグラフィー技術を用いた。
[用語6]: 力学系理論：時間とともに変化する系の状態を記述する微分方程式などの解の性質を予測する理論体系。パラメーターを変化させた際の解の不安定化（分岐）の分類やカオス現象の解析を行うことができる。
[用語7]: 自己駆動粒子：遊泳バクテリアや自己駆動コロイド、あるいは数理モデルにおいて考える動き回るエージェントなど、自ら動く能力を持った物体の総称。駆動原理にかかわらず同様の粒子として捉えることで、普遍的な性質を抜き出そうとする物理学の考え方を反映した呼称である。

論文情報

掲載誌：: Proceedings of National Academy of Science USA
タイトル：: Vortex reversal is a precursor of confined bacterial turbulence
著者：: Daiki Nishiguchi, Sora Shiratani, Kazumasa A. Takeuchi, Igor S. Aranson
DOI：: 10.1073/pnas.2414446122